近日，我校激光光谱研究所肖艳红教授研究团队与我校申恒教授、丹麦奥胡斯大学克劳斯·莫尔莫(Klaus Mølmer)教授开展合作研究，证明了位置和动量的测量结果的不确定度可低于由著名海森堡不确定关系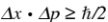所设定的极限，研究结果以 “Retrodiction beyond the Heisenberg uncertainty relation”为题于2020年11月9日发表在《自然·通讯》（Nature Communications）上。论文的第一作者为我校包晗博士，共同通讯作者为肖艳红教授、申恒教授和克劳斯·莫尔莫 (Klaus Mølmer)教授。

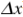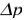根据合作团队的描述，当讨论量子力学的不确定性时，真正讨论的不是粒子的位置和速度的概率分布，而是能够多么准确地预测实验结果。量子力学的波函数提供了获得特定实验结果的概率，并且很容易证明，位置和动量的测量结果的不确定度应当遵循海森堡不确定关系。然而，当我们考虑另外一种情形，也就是允许测量结束之后接着继续获取测量信息(称为“回溯测量”)时，需要用克劳斯·莫尔莫提出的另一套理论【Phys. Rev. A 96, 062131 (2017)】来描述这种情况。此时，对于之前的位置或动量的测量结果的估计，其不确定度不受海森堡不确定关系的限制。肖艳红教授研究团队利用近室温的铷原子蒸气池进行了实验研究，所获得的和的乘积为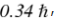，小于海森堡不确定关系中的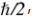，并且这个乘积在理论上没有下限。本工作除了阐明量子力学的基本问题之外，所实现的实验中不确定度的降低还可以应用于量子精密测量，例如突破标准量子极限的高灵敏度原子磁力计，该实验结果由同一团队在今年5月发表于《自然》杂志【Nature 581, 159 (2020)】。团队成员还包括复旦大学物理学系博士研究生金沈超，段俊磊等。

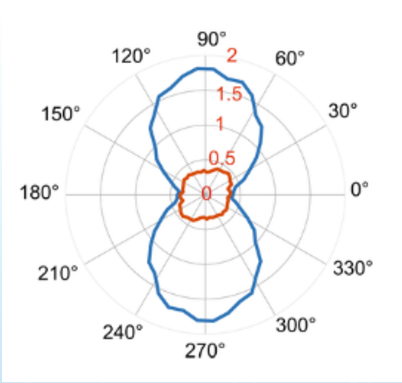
图：蓝色和红色曲线显示了位置测量（水平方向）和动量测量（垂直方向）以及这两个量的任意线性组合（其他方向）的测量方差。蓝色曲线显示基于传统预测的结果，它遵循海森堡不确定度关系；因此，位置的方差被压缩到0.5（标准量子极限）以下，但伴随着动量不确定度的增加。红色曲线显示，当同时使用预测和回溯的测量结果时，对于位置和动量的测量结果的估计（以及它们的任何线性组合）方差可以都减小。

该项目受到科技部重点研发计划、国家自然科学基金委“精密测量物理”重大研究计划、山西大学量子光学与光量子器件国家重点实验室、复旦大学应用表面物理国家重点实验室、复旦大学微纳光子结构教育部重点实验室、极端光学省部协同创新中心（山西大学）等的资助。

      论文链接：https://doi.org/10.1038/s41467-020-19495-1